Modell: Bewegung eines Körpers im Kraftfeld eines Zentralkörpers

tm.jpg 7, Thema „Geschwindigkeit und Beschleunigung“, S. 78 - 79

Screenshot: A. Nussbaumer

Physikalische Grundlagen:

Das Newton'sche Gravitationsgesetz beschreibt die Kraft zwischen Massen:

tex:F(M,m,r) = G \cdot \frac{M \cdot m} {r^2}

Diese Gravitationskraft F hängt also von den Massen M und m der beiden Körper und von ihrer Entfernung r ab. G ist die Gravitationskonstante.

Die Gravitationskraft ist eine gerichtete Größe. Sie wirkt stets anziehend zwischen den beiden Massen M und m. Ihre Richtung wird durch den Radiusvektor tex:\vec r beschrieben:

tex:\vec F (M,m,\vec r) = G \cdot \frac {M \cdot m} {r^2} \cdot \frac {\vec r} r

In der vektoriellen Formel ist der Einheitsvektor tex:\vec r_0 des Radiusvektors tex:\vec runschwer zu erkennen. Er legt die Richtung der Gravitationskraft tex:\vec F fest, während der Betrag der Gravitationskraft durch das (skalare) Gravitationsgesetz angegeben wird.

Vereinfachtes Modell:

Für unser Modell untersuchen wir grundsätzlich das „1/r² - Kraftgesetz“. Wir gehen von einem Zentralkörper mit großer Masse M (im GeoGebra-Beispiel als „Erde“ bezeichnet) und von einem zweiten Körper mit der Masse m aus, der sich im Kraftfeld des Zentralkörpers bewegt („Satellit“. So können wir die Bewegung des Zentralkörpers vernachässigen. Weiters wählen wir im Gravitationsgesetz für das Produkt der beiden Unveränderlichen G und M (willkürlich) den Wert 1. Damit vereinfacht sich das Gravitationsgesetz zu:

tex:\vec F(m,\vec r) = \frac m {r^2} \cdot \vec r_0

Die Kraft auf den Satelliten bewirkt eine Beschleunigung tex:\vec a. Aus der Bewegungsgleichung tex:\vec F = m \cdot \vec a erhalten wir für den Beschleunigungsvektor tex:\vec a:

tex:\vec a = \frac {\vec F} m

Setzen wir für den Kraftvektor tex:\vec F aus dem Gravitationsgesetz ein, so erhalten wir

tex:\vec a = \frac m {r^2} \cdot \vec r_0 \cdot \frac 1 m = \frac 1 {r^2} \vec r_0

Das ist nun wirklich einfach geworden!

n unserem Modell untersuchen wir also, wie sich ein (kleiner) Körper in einem „1/r² - Feld“ bewegt.

Arbeiten mit Differenzengleichungen

Aus den Definitionen für Geschwindigkeit und Beschleunigung wissen wir:

tex:\frac {d \vec s(t)} {dt} = \vec v(t)

tex:\frac {d \vec v(t)} {dt} = \vec a(t)

Wir haben zu jeden Zeitpunkt t (also „momentan“) den Beschleunigungsvektor tex:\vec a aus dem Massenanziehungsgesetz zur Verfügung. Aus dem momentanen tex:\vec a berechnen wir den momentanen Geschwindigkeitszuwachs tex:d \vec v und daraus die resultierende (monentane) Geschwindigkeit tex:\vec v = \vec v_{alt} + d \vec v.

Aus dem momentanen Geschwindigkeitsvektor tex:\vec v bestimmen wir die momentane Verschiebung tex:d \vec s für den Satelliten und somit die aktuelle Position tex:\vec s = \vec s_{alt} + d \vec s.

Hinweis: In der Oberstufe hast du mit Differenzengleichungen zu arbeiten gelernt, bei denen Differenzen von ungerichteten Größen aufgetreten sind. Hier werden die gleichen Überlegungen für (zweidimensionale) Vektoren verwendet. Wie für ungerichtete Größen bietet sich die Tabellenkalkulation an: In die Zellen tragen wir einfach die Vektoren ein (ein Lob auf GeoGebra ;-) !).

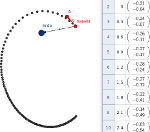
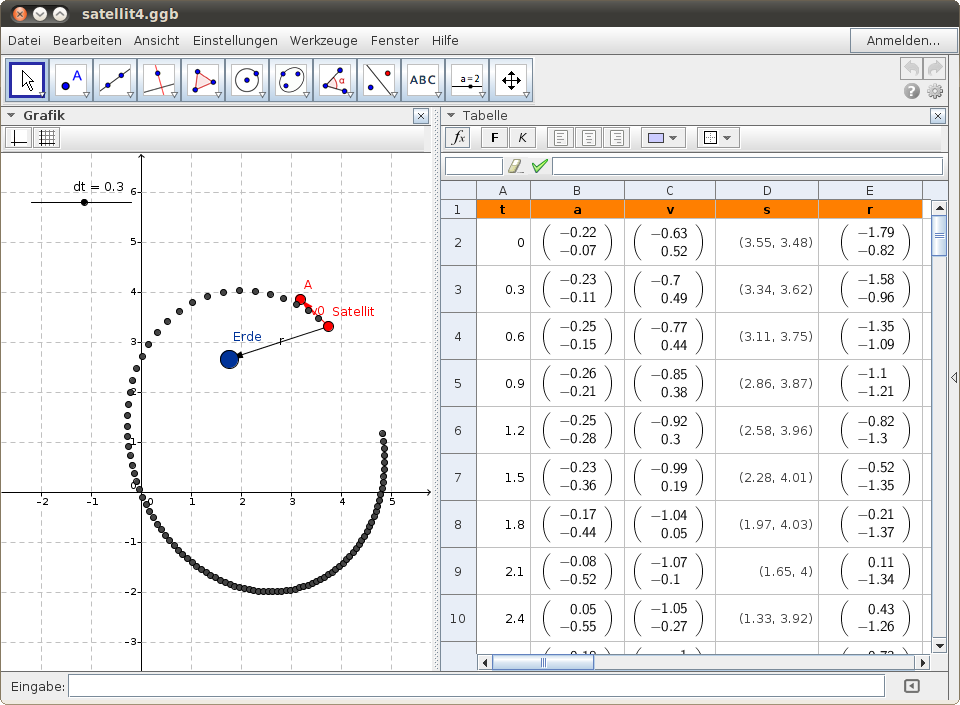
Im folgenden GeoGebra-Applet wird die Position eines Satelliten in bestimmten Zeitschritten dt ermittelt. Wähle eine Position für den Zentralkörper und eine Startposition für den Satelliten. Die Größe und die Richtung für die Anfangsgeschwindigkeit des Satelliten wird durch den Vektor tex:\vec v_0 angegeben. Lege seine Größe durch Ziehen am Punkt A fest:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Lege die Größe für den Zeitschritt dt mit dem Schieberegler fest. Untersuche, welche Auswirkungen eine Veränderung des Zeitschritts dt hat!
  • Gib die Formel für den Geschwindigkeitsvektor für den Zelleintrag in der Tabellenansicht an!
  • Gib die Formel für den Ortsvektor für den Zelleintrag in der Tabellenansicht an!
  • Untersuche den physikalischen Kontext des Modells: Abhängig von der Startposition tex:\vec s_0 des Satelliten und abhängig von seiner Anfangsgeschwindigkeit tex:\vec v_0 umläuft der Satellit den Zentralkörper auf einer Ellipsen- oder Hyperbelbahn. Untersuche diese Bewegungsformen!

Hinweis: Um die Position des Satelliten bei gleichbleibendem Geschwindigkeitsvektor zu verändern, markiere sowohl den Satelliten als auch die Pfeilspitze A und ziehe beide zusammen in die neue Position …

Zurück zu Geschwindigkeit und Beschleunigung

Weiter zu Modell: Doppelsternsystem


Zuletzt angesehen: • satellit