Inhaltsverzeichnis
Maxima: Kurven und Flächen im Raum
Die gute Darstellung von Raumkurven und Flächen ist eine interessante Herausforderung! Es ist günstig, wenn du die Aufgaben auf deinem Computer ausführen kannst - maxima und Gnu-Plot stehem dir dazu kostenlos zum Download zur Verfügung.
Tipp: Kopiere die komplizierten Ausdrücke direkt von der Webseite in die maxima-Eingabe!
Arbeitsblatt: Schnittpunkte dreier Kugeln
Bereits in der 6. Klasse hast du Geraden im Raum und Ebenen in Parameterdarstellen kennen gelernt:
Geraden
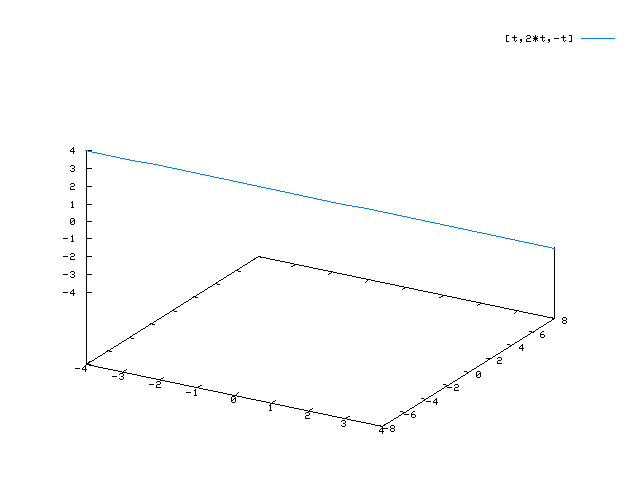
Die Gerade g: X(t) = (0|0|0) + t (1|2|-1) verläuft durch den Koordinatenursprung und hat den Richtungsvektore (1|2|-1):
x(t) = t y(t) = 2t z(t) = -t
plot3d([t,2*t,-t],[t,-4,4],[u,-4,4],['grid,20,20]);
Überprüfe die korrekte Darstellung dieser Geraden im folgenden maxima-Output:
Ebenen
Die Ebene wird durch einen Anfangspunkt (Einstiegspunkt) und mit zwei Richtungsvektoren mit je einem Parameter beschrieben:
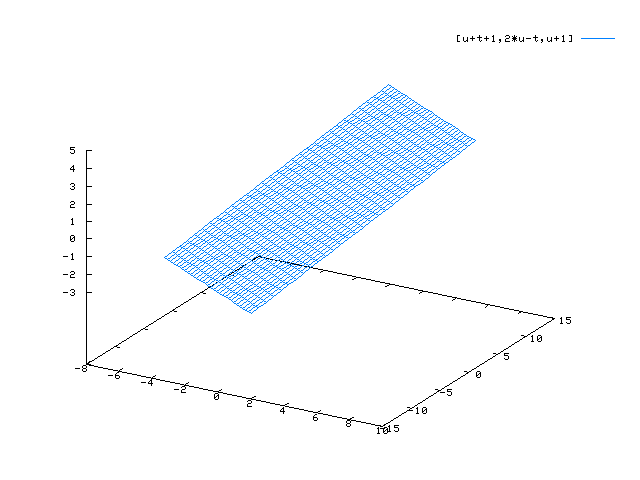
Ebene: X(t) = (1|0|1) + t (1|-1|0) + u (1|2|1)
x(u,v) = 1 + u + v y(u,v) = - u + 2v z(u,v) = 1 + v
plot3d([1+u+v, -u+2*v, 1 + v],[u,-4,4],[v,-4,4]);
Lagebeziehungen
Tangentialebenen
Kurven im Raum
Analog zur Parameterdarstellung in der Ebene stellen wir Kurven im Raum dar; dabei verwenden wir zusätzlich eine Beschreibung der z-Koordinate:
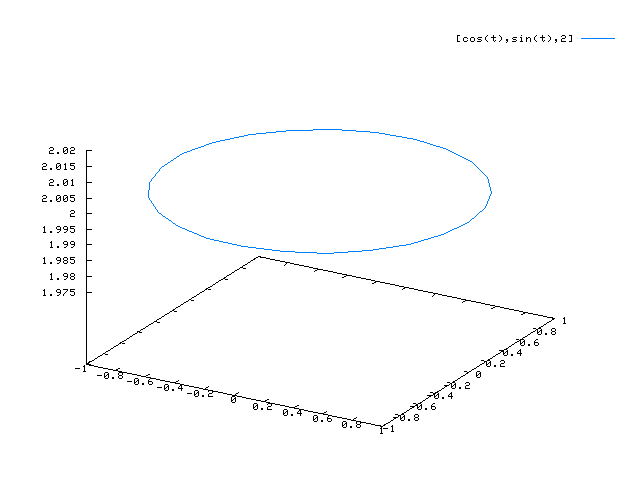
Beispiel: Kreislinie in einer horizontalen Ebene
x(t) = cos(t) y(t) = sin(t) z(t) = 2
plot3d([cos(t), sin(t), 2],[t,0,2*%pi],[u,0,2*%pi],['grid,100,2]);
Beispiel: Schraubenlinie (Helix)
Beachte den Unterschied zur Kreislinie: Die z-Koordinate wächst mit dem Parameter t und verschiebt die Punkte der Kreislinie nach oben …
x(t) = cos(t) y(t) = sin(t) z(t) = t
plot3d([cos(t), sin(t), -12 + t],[t,0,8*%pi],[u,0,2*%pi],['grid,100,2]);
Untersuche an Hand der GeoGebra-Animation, wie die Helix entsteht!
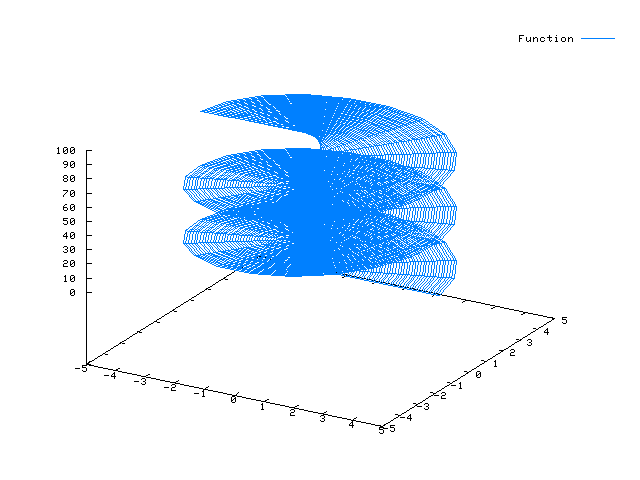
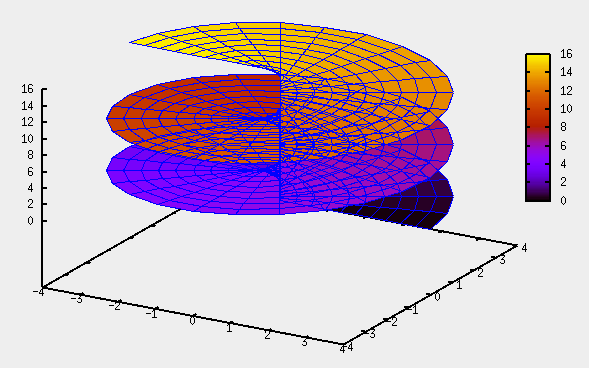
Beispiel: Schraubenlinie auf einer Kegelfläche
Beachte den Unterschied zur Helix: Der Radius fällt mit der monoton fallenden linearen Funktion (4 - t/8)…
x(t) = cos(t) * (4 - t/8) y(t) = sin(t) * (4 - t/8) z(t) = t
plot3d([cos(t)*(4-t/8), sin(t)*(4-t/8),t],[t,0,8*%pi],[u,0,1],['grid,100,2]);
Weitere Bilder:
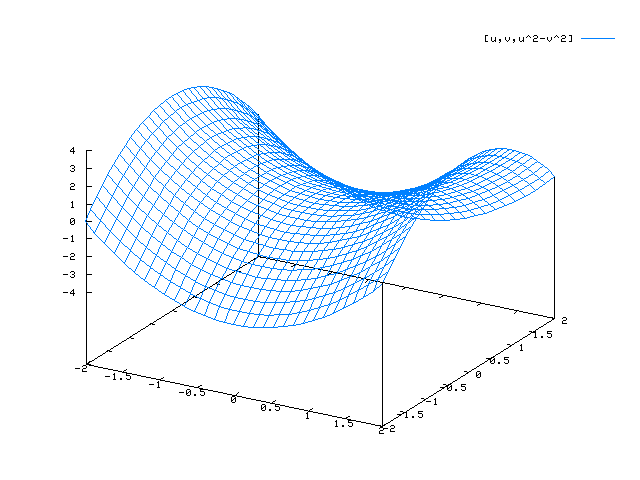
Flächen im Raum
Die Flächen werden durch zwei Parameter, z.B. durch die Parameter u und v beschrieben. Beachte genau die Zuordnung zu den drei Raumkoordinaten!
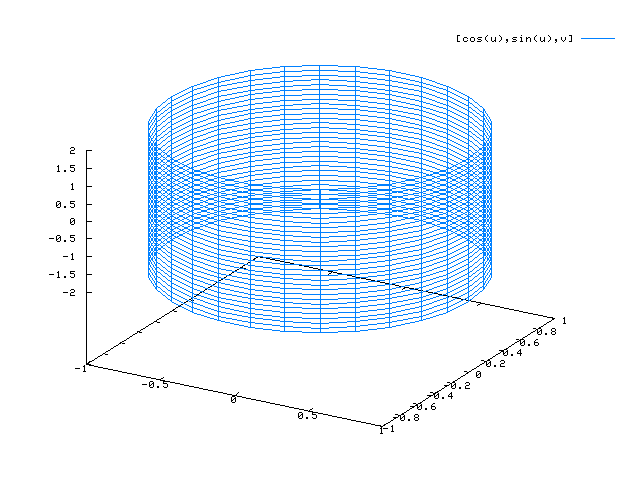
Beispiel: Zylinderfläche
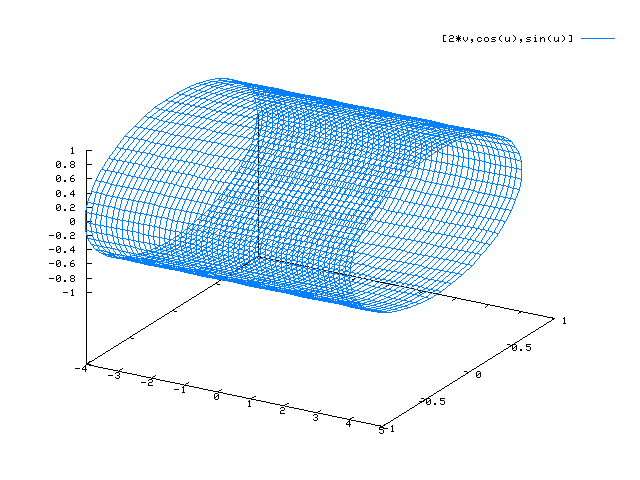
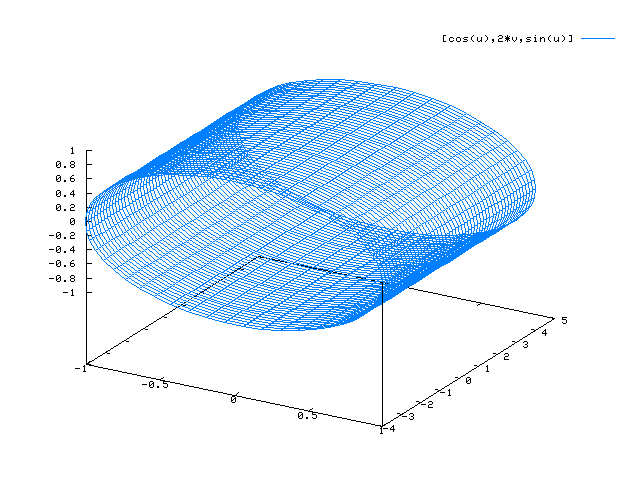
x(u,v) = cos(u) y(u,v) = sin(u) z(u,v) = v
plot3d([cos(u),sin(u),v],[u,0,2*%pi],[v,-2,2]);
Beachte genau die Intervalle, für die die Paramter u und v definiert sind!
Untersuche, wie die Zylinderfläche in der GeoGebra - Animation zustande kommt!
Weitere Beispiele:
Beispiel: Kegelfläche
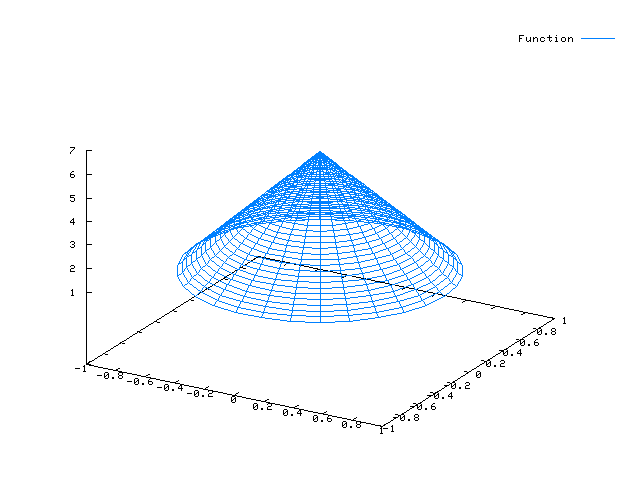
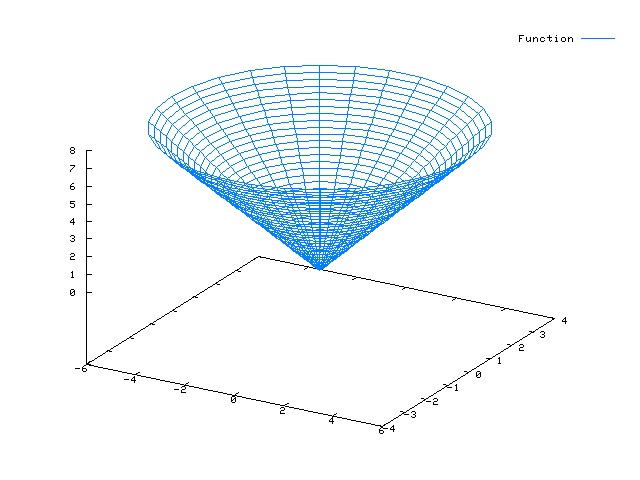
Beachte den Unterschied zur Zylinderfläche: Der Radius nimmt mit (1 - v/6) ab (lineare Funktion)…
x(u,v) = cos(u)*(1 - v/6) y(u,v) = sin(u)*(1 - v/6) z(u,v) = v
plot3d([cos(u)*(1-v/6), sin(u)*(1-v/6), v],[u,0,2*%pi],[v,1,6]);
Weitere Beispiele:
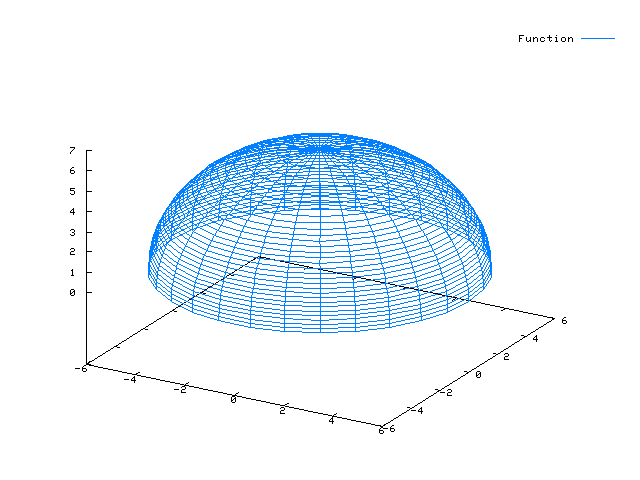
Beispiel: Kugelfläche
Beachte den Unterschied zur Zylinderfläche: Der Radius nimmt mit sqrt(36 - v^2) ab (Quadratwurzelfunktion)…
x(u,v) = cos(u)*sqrt(36 - v^2) y(u,v) = sin(u)*sqrt(36 - v^2) z(u,v) = v
plot3d([cos(u)*sqrt(36 - v^2), sin(u)*sqrt(36 - v^2), v],[u,0,2*%pi],[v,0,6]);
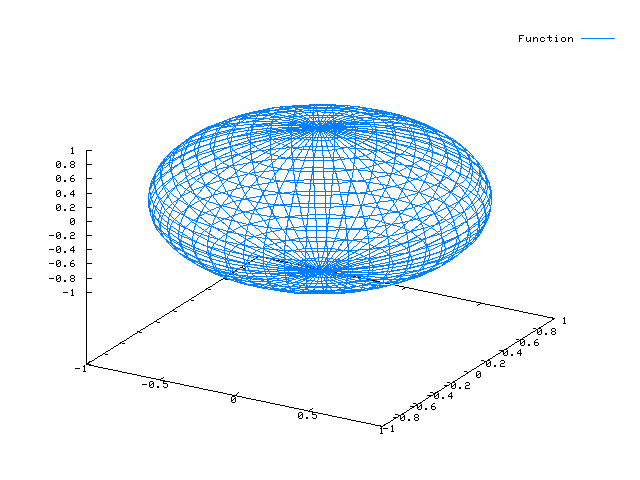
Die „Einheitskugel“ kannst du mit folgender Parametrisierung darstellen:
x(u,v) = cos(u) * cos(v) y(u,v) = sin(u) * cos(v) z(u,v) = sin(v)
plot3d([cos(u) * cos(v), sin(u) * cos(v), sin(v)], [u, 0, 2*%pi], [v, 0, 2*%pi]);
Weitere Beispiele:
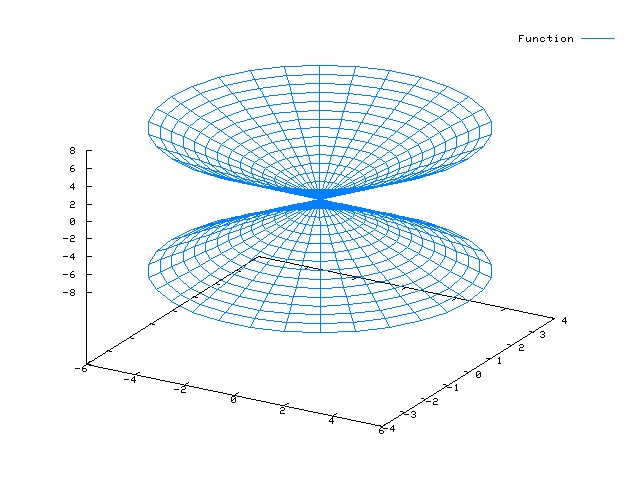
Beispiel: Hyperboloid
Beachte den Unterschied zur Zylinderfläche: Der Radius nimmt mit 1/v ab (Hyperbel)…
x(u,v) = cos(u) / v y(u,v) = sin(u) / v z(u,v) = v
plot3d([cos(u)/v, sin(u)/v, v],[u,0,2*%pi],[v,1,6]);
Weitere Beispiele:
Beispiel: Torus
Erinnere dich:
x(u,v) = cos(u)*6 y(u,v) = sin(u)*6 z(u,v) = 2
Damit erhalten wir einen Kreis mit Mittelpunkt M(0|0|2), Radius r = 6, der in der horizontalen Ebene z = 2 liegt.
Mit
x(u,v) = cos(u)*(6 + 2*cos(v)) y(u,v) = sin(u)*(6 + 2*cos(v)) z(u,v) = 2 + 2*sin(v)
erhalten wir eine Fläche, die durch einen um die obige Kreislinie „rotierenden“ Kreis mit Radius r = 2 entsteht. Sein Mittelpunkt liegt auf der ursprünglich festgelegten horizontalen Kreislinie mit Radius r = 6 …
plot3d([cos(u)*(6 + 2*cos(v)), sin(u)*(6 + 2*cos(v)), 2 + 2*sin(v)], [u,0,2*%pi], [v,0,2*%pi], ['grid, 50,50]);
Weitere Beispiele:
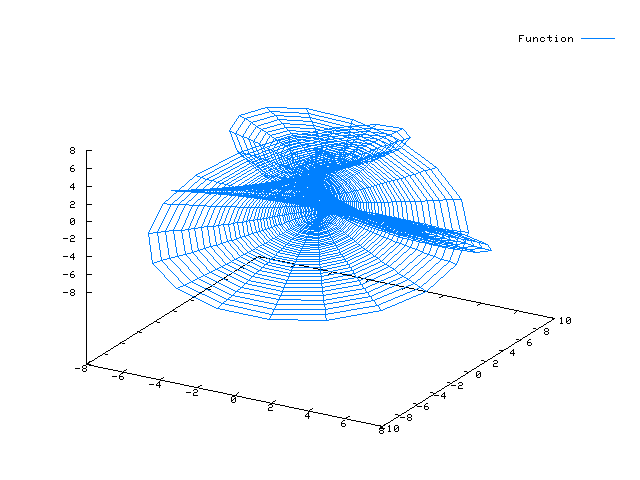
Zum Artikel Die Wendelfläche (GeoGebra-Animation)
Weiter zu Lernpfad Maxima - plot3d | Lernpfad GeoGebra - Grafik 3D | Kurven und Flächen im Raum