Inhaltsverzeichnis
Dynamische Systeme
 8, S. 121 - S. 152, Themenheft Mathematik mit GeoGebra 7-8, S. 30 - S. 31
8, S. 121 - S. 152, Themenheft Mathematik mit GeoGebra 7-8, S. 30 - S. 31
Dynamische Systeme können in diskreten Zeitschritten in Differenzengleichungen berechnet werden (beispielsweise mit der Tabellenkalkulation) oder kontinuierlich mit Hilfe von Differentialgleichungen gelöst werden. Mit GeoGebra können diese Differentialgleichungen numerisch (Algebra-Ansicht) oder exakt (CAS-Ansicht) gelöst werden.
Numerische Lösung (Algebra-Ansicht)
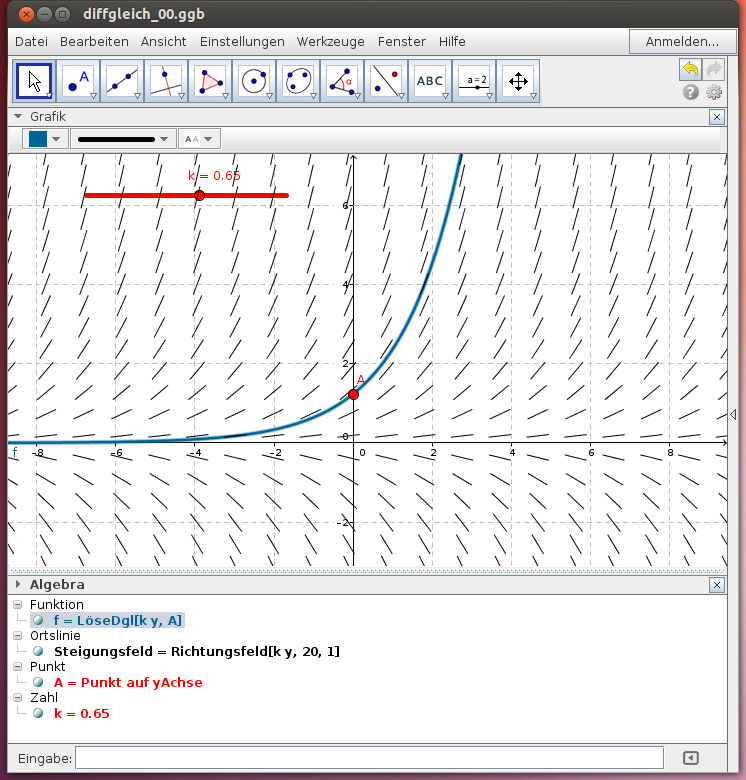
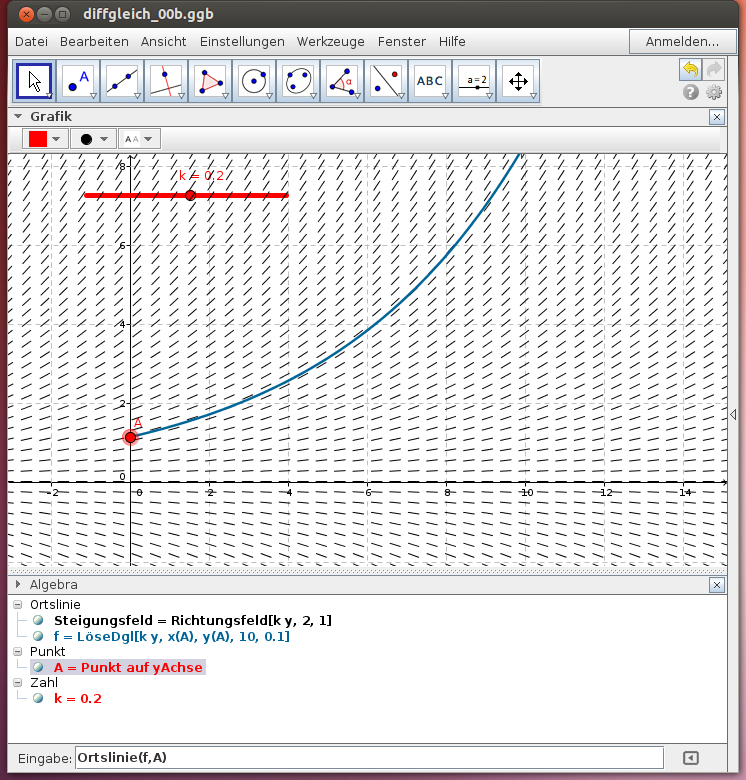
Mit GeoGebra stellen wir bei kontinuierlichen Modellen passend zu einer Funktion in zwei Variablen ein Richtungsfeld dar, wählen den Anfangswert durch den Punkt A und stellen die Lösungsfunktion dar. Die Differentialgleichung (oder
) wird dabei als Funktion in den beiden Variablen x und y eingegeben (vgl. Themenheft GeoGebra 7-8 - Dynamische Systeme).
Beispiel: Die lineare Differentialgleichung y' = k y
Lineares Wachstumsmodell
Exponentielles Wachstumsmodell
Beschränktes Wachstumsmodell
- Abkühlkurve (beschränktes Modell)
- Temperaturausgleich (beschränktes Modell)
- Fischpopulation (logistisches Modell)
Differentialgleichungen bei Bewegungsvorgängen
Differenzengleichungen sind - etwa bei zweidimensionalen Modellen zur Bewegung eines Körpers in einem Kraftfeld - auch für Vektoren möglich. So wird etwa die Position eines Körpers nach einem Zeitschritt
aus seiner (momentanen) Geschwindigkeit
mit einer Differenzengleichung für Vektoren berechnet:
Solche iterativen Berechnungen mit Vektoren sind natürlich eine hübsche Anwendung in der Tabellenansicht!
Numerisches Lösen von Differentialgleichungen
Systembeschreibung durch Wirkungsdiagramme
Systembeschreibung durch Flussdiagramme
Exakte Lösung (CAS-Ansicht)
GeoGebra stellt in der CAS-Ansicht den Befehl LöseDgl(<y'>,P) zur Verfügung, der versucht eine exakte Lösung der gewöhnlichen Differentialgleichung erster und zweiter Ordnung zu finden.
- Temperaturausgleich (beschränktes Modell)
- Fischpopulation (logistisches Modell)