Dies ist eine alte Version des Dokuments!

Volumsberechnung

tm.jpg 8, S. 52 - 53

Rotationskörper entstehen, wenn sich Kurven um 360° um eine Achse drehen. Diese Drehung kann in der GeoGebra Grafik 3D-Ansicht mit dem GeoGebra-Befehl Drehe(<Kurve>,<Winkel>,<Achse>) dargestellt werden.

Das Volumen Vy einer Körpers, der durch Rotation des Graphen von f(x) über dem Intervall [y1; y2] um die y-Achse entsteht, ist durch das bestimmte Integral

tex:V_y = \pi \cdot \int_{y_1}^{y_2} x^2 dy, tex:x = f^{-1}(y) gegeben.

Beispiel: Ein Rotationskörper entsteht durch Rotation des von den Koordinatenachsen und von den folgenden Kurven begrenzten Flächenstückes:

  • tex:f(x) = \sqrt {x^2 - 1}
  • tex:g(x) = 2 + \frac {x^2} 4
  • tex:h(x) = 3

Berechne sein Volumen!

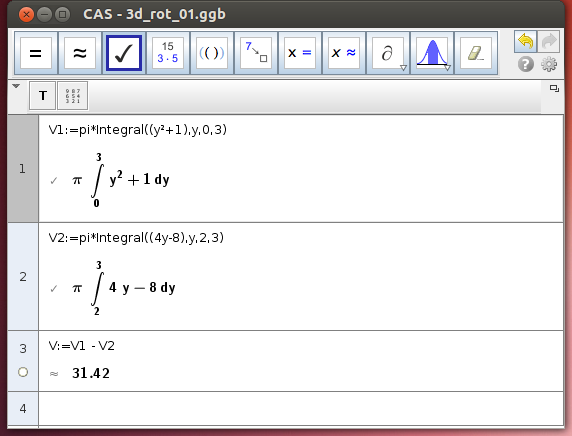
Wir stellen die Kurven und ihre Rotation um die y-Achse in der Grafik 3D-Ansicht dar und berechnen die bestimmten Integrale:

Screenshot: Alfred Nussbaumer

Für die Umkehrfunktionen erhalten wir:

  • tex:f^{-1}: x^2 = y^2 + 1
  • tex:g^{-1}: x^2 = 4y - 8

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Ergebnis: V ≈ 31,42

Zurück zu Anwendungen der Integralrechnung


Zuletzt angesehen: • 3d_rot_01